Fast + Slow Pointers (Floyd’s Cycle Detection)

Slow and fast pointers race

This technique uses two pointers moving at different speeds called slow and fast, to detect cycles in a sequence of nodes, most commonly in linked lists.

You’ll want to reach for this pattern any time you need to figure out if your linked list loops back on itself. Maybe you’re stuck with a list that seems to go on forever and you’re not sure why. With this, you can tell if there’s a cycle hiding in there, you can also follow a simple extra step to find where that cycle starts. Once you spot the start of the cycle, everything about debugging gets simpler, and you start to see the shape of your data a lot more clearly.

def has_cycle(head):
    slow = fast = head
    while fast and fast.next:
        slow = slow.next                # 1 step
        fast = fast.next.next           # 2 steps
        if slow == fast:
            return True
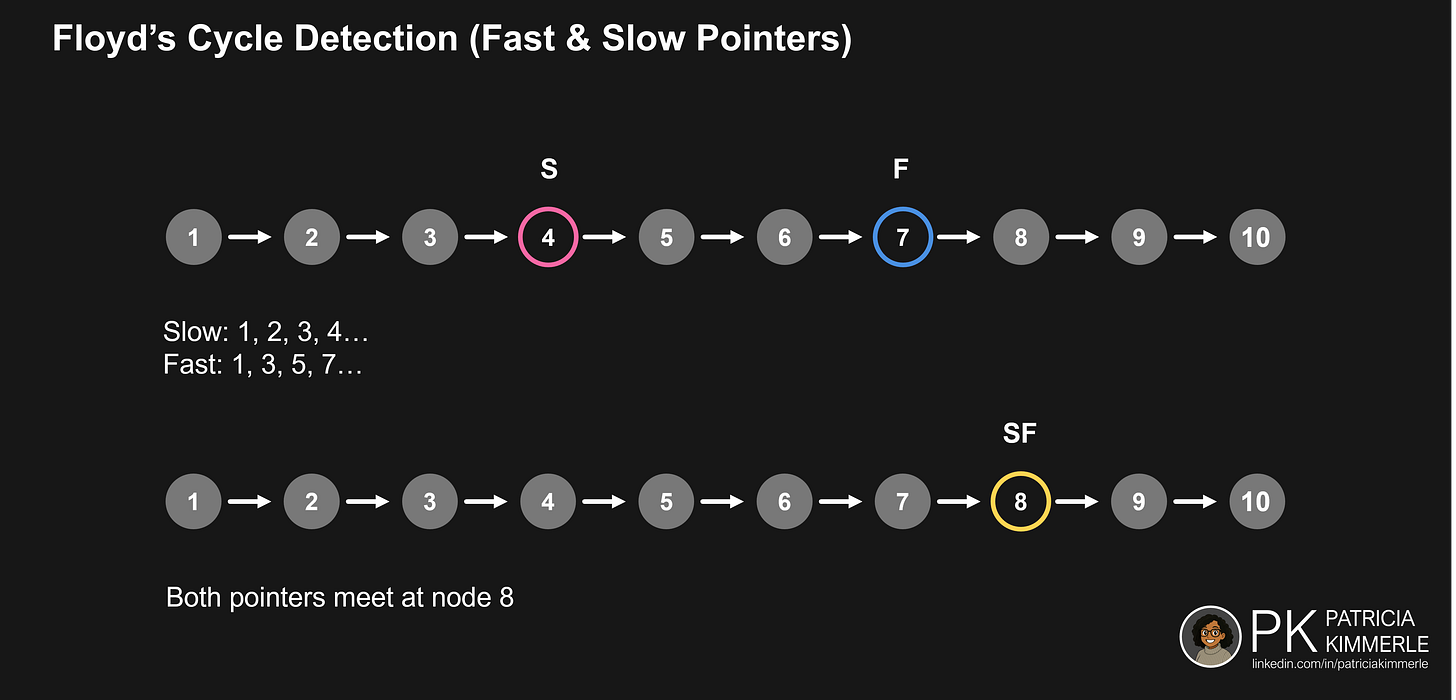
    return False

Visual walkthrough of Floyd’s Cycle Detection

Both pointers start at the very first node, side by side. Slow takes 1 step at a time and the fast pointer takes 2 (2:1 ratio). That double speed is what creates the chase. When the fast pointer gets to node 9, its next move takes it to node 10, but 10 isn't the end. It loops back to node 4, because node 10 points right back into the cycle. That's why you don't see the fast pointer stopping at node 10 or continuing to so to some node 11 (there is no 11). It's caught in the cycle now, moving around with the slow pointer until, eventually, they land on the same node.

class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None
        
def has_cycle (head):
    slow = fast = head
    while fast and fast.next:
      slow = slow.next                # 1 step
      fast = fast.next.next           # 2 steps
      if slow == fast:
          return True
    return False
    
# build a track
a = ListNode(1)
b = ListNode(2)
c = ListNode(3)
d = ListNode(4)
a.next = b
b.next = c
c.next = d
d.next = b # loops back to node 2

print("Cycle found?", has_cycle(a)) # should print True

Think of a classic Mario Kart track. You and your friend start driving side by side. Your friend grabs every speed boost and pulls ahead. If the track just goes straight from start to finish, you never see them again because they cross the line first and that’s it. But if the track loops in a big circuit, like most Mario Kart races, your friend will eventually lap you and zoom by from behind. When that happens, you both know you’re on a loop.

That's Floyd's algorithm with fast and slow pointers. If the list never loops back, the fast pointer just keeps going and never meets the slow one. But if there’s a cycle, the fast one always catches up. When they meet, that’s your proof there’s a loop in your list.